e already
introduced the mesh
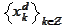 in the previous section.
in the previous section.
Given
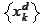 ,
the index
,
the index
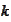 is called the "location index" and the index
is called the "location index" and the index
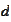 is called the "scale" index.
is called the "scale" index.
Note
that
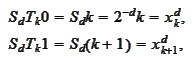
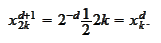 We introduce the notations
We introduce the notations
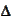 ,
,
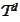 ,
,
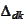 ,
,
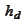 ,
,
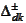 :
:
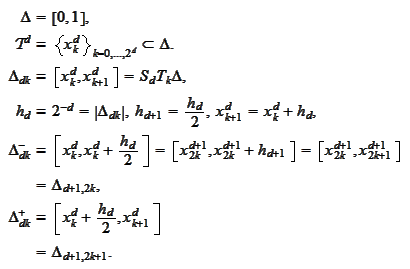
Note
that
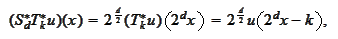
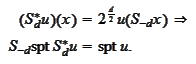 Read the above
"
Read the above
"
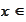 spt
spt
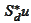 (see
(see
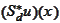 )
iff
)
iff
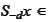 spt
spt
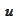 (see
(see
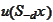 )".
Consequently
)".
Consequently
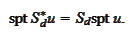 Similarly,
Similarly,
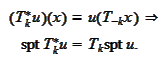 We
conclude
We
conclude
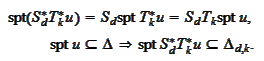
|
|
(Property of scale and transport 1)
|
In
addition,
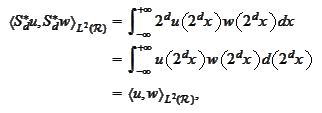
|
|
(Property of scale and transport 2)
|
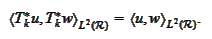
|
|
(Property of scale and transport 3)
|
In the following sections we frequently use Fourier transform
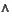 as well as the operations
as well as the operations
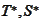 .
We investigate the
interaction:
.
We investigate the
interaction:
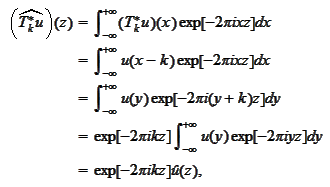
|
|
(Property of scale and transport 4)
|
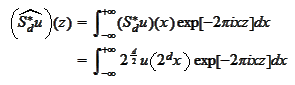 We make a change
We make a change
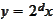 ,
,
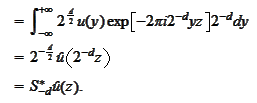
|
|
(Property of scale and transport 5)
|
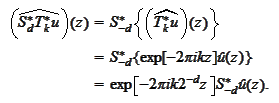
|
|
(Property of scale and transport 6)
|
We investigate transposition of
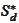 and
and
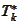 :
:
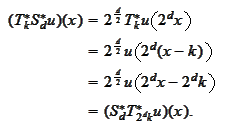
|
|
(Property of scale and transport 7)
|
|