et
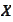 and
and
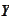 are separable Hilbert spaces,
are separable Hilbert spaces,
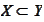 ,
,
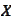 is dense in
is dense in
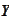 and the natural injection operator
and the natural injection operator
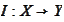 ,
,
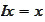 is continuous
(
is continuous
(
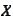 topology is stronger:
topology is stronger:
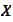 -convergence
implies
-convergence
implies
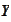 -convergence).
We denote such
relationship
-convergence).
We denote such
relationship
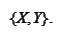 Consider the
form
Consider the
form
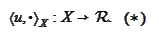 Let
Let
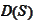 be the set of
be the set of
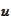 such that the form
such that the form
 is continuous in
is continuous in
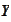 topology.
topology.
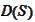 is dense in
is dense in
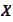 with respect to
with respect to
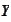 topology. By denseness of
topology. By denseness of
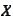 in
in
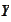 the form extends to
the form extends to
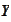 .
Therefore, by the proposition (
Riesz
representation theorem
) for any
.
Therefore, by the proposition (
Riesz
representation theorem
) for any
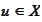 there is an element
there is an element
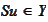 such
that
such
that
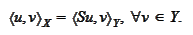 The
The
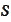 is a linear operator
is a linear operator
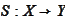 unbounded in
unbounded in
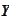 topology.
Furthermore,
topology.
Furthermore,
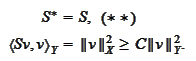 By
By
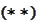 ,
continuous functions of
,
continuous functions of
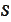 are well defined. In particular, the operator
are well defined. In particular, the operator
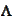
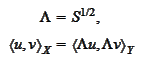 is well defined. We
introduce
is well defined. We
introduce
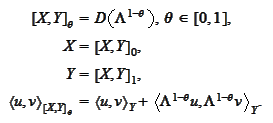
Proposition
(Interpolation inequality) Given
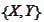 we
have
we
have
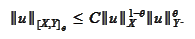
|