e hinted on several occasions that model-consistent pricing of large variety
of financial instruments is neither possible nor necessary. However, one still
needs to install consistent hedges. In this section we describe an intuitive
technique for calculation of such hedges. The presentation is based on
[Cherny2006]
.
We are working in the setup described by
(
Finite space variable
incomplete market
). However, we assume that there are several participants
on the market (or several trading desks participating in a structured trade)
using the sets of valuation measures
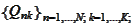with the index
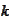being the participant index and
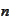being the model index. The trade
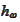is an acceptable opportunity if it may be represented as
sum
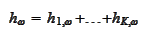with each component
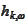being acceptable in the sense of the previous section and with respect to
.
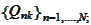We already remarked in the previous section that the pricing technique of the
formulas (
Incomplete market
ask
),(
Incomplete market bid
)
represent the coherent measure pricing. The coherent measure
(
Coherent measure
) may be regarded as the
support function (
Support function
). It
remains to point out that we operate in the situation of the infimal
convolution (
Infimal convolution
). We
combine the results
(
Existence of incomplete
market pricing
),(
Incomplete market
ask
),(
Incomplete market bid
) and the
result (
Infimal
convolution of support functions
) and arrive to the version of the
statement (
Incomplete market
ask
),(
Incomplete market bid
) with
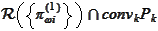replaced for
.
|
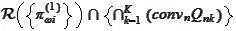