he fundamental solution
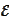 for the heat
operator
for the heat
operator
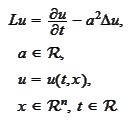 takes the
form
takes the
form
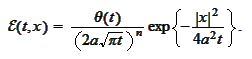 Here the
Here the
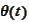 is the step function (see the formula (
step
function
)). Using the
fact
is the step function (see the formula (
step
function
)). Using the
fact
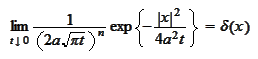 one can verify directly
that
one can verify directly
that
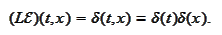
Problem
Consider the
problem
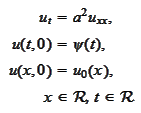 where the functions
where the functions
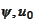 are smooth.
are smooth.
Problem
Consider the
problem
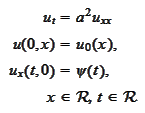 where the functions
where the functions
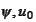 are smooth.
are smooth.
|