et
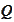 be the interval
be the interval
![$\left[ 0,1\right] $](graphics/notesCF__1__2901.gif) with point
with point
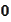 and point
and point
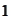 made identical. In other words, a function
made identical. In other words, a function
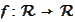 is well defined on
is well defined on
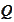 if and only if it has the
property
if and only if it has the
property
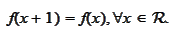
Notation
For a sequences
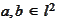 we use the
notations
we use the
notations
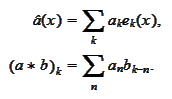
Proposition
For
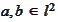 we
have
we
have
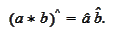
Using results of the section
(
Fourier analysis in
Hilbert space section
) we state that for
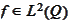 there
is
there
is
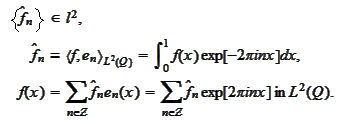
Such result expands to
![$\left[ 0,a\right] $](graphics/notesCF__1__2921.gif) :
:
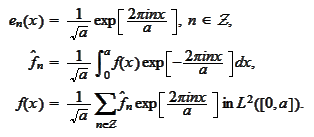
The
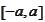 version
is
version
is
|