Proof
For
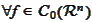 we
calculate
we
calculate
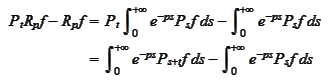 We make the change
We make the change
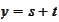 in the first
integral.
in the first
integral.
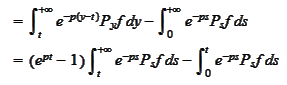
It follows from (1) that
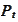 is a linear operator in
is a linear operator in
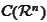 and we conclude from the definition of
and we conclude from the definition of
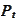 that
that
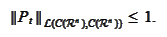
Hence, for
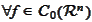
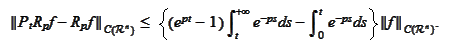 Therefore
Therefore
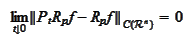 thus
thus
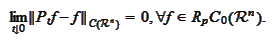 In view of the proposition
(
Properties of Feller resolvent
1
)-3, it remains to prove that
In view of the proposition
(
Properties of Feller resolvent
1
)-3, it remains to prove that
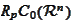 is dense in
is dense in
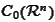 .
We
evaluate
.
We
evaluate
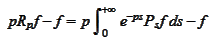 for large
for large
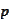 and aim to show that the quantity is small. We make a change
and aim to show that the quantity is small. We make a change
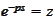 in the integral,
in the integral,
 ,
,
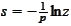
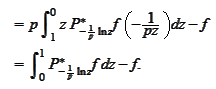 The quantity
The quantity
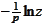 is positive and tends to 0 when
is positive and tends to 0 when
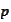 tends to
tends to
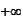 .
Hence, using
(2),
.
Hence, using
(2),
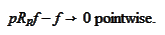 In
addition
In
addition
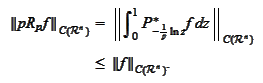 Therefore, by the proposition
(
Dominated convergence theorem
),
for any finite measure
Therefore, by the proposition
(
Dominated convergence theorem
),
for any finite measure
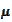
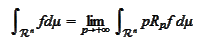 Hence, if the measure
Hence, if the measure
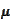 vanishes
on
vanishes
on
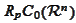 then it vanishes on
then it vanishes on
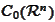 .
Thus,
.
Thus,
 is dense in
is dense in
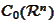 .
.
Proposition
(Properties of Feller resolvent
2) Let
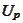 be a resolvent of a Feller process. We
have
be a resolvent of a Feller process. We
have
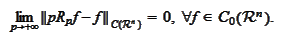
|