here is a way to solve a three-diagonal finite difference scheme with an
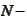linear
number of algebraic operations. Suppose some finite difference scheme takes
the
form
|
|
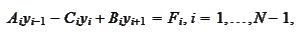
(Factorization1)
|
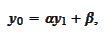
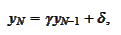with the
properties
|
|
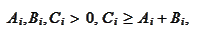
(Factorization3)
|
|
|
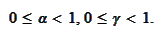
(Factorization4)
|
We look for a recursive
relationship
|
|
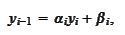
(Factorization2)
|
with some coefficients
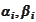that we determine through the substitution into the scheme
(
Factorization1
):
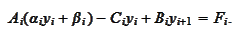We express all the
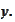through
the
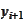using the relationship
(
Factorization2
):
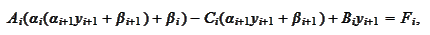
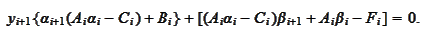Hence, to satisfy the (
Factorization1
) we must
have
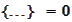and
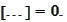Such conditions lead to the recursive
relationships
|
|
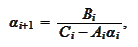
(Factorization5)
|
|
|
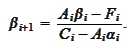
(Factorization6)
|
Under conditions
(
Factorization3
),(
Factorization4
)
we
have
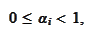
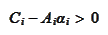for all
.
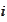Therefore, we start
with
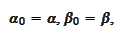and produce
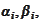
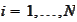according to the
(
Factorization5
),(
Factorization6
).
At the final step of the iteration we use the boundary
condition
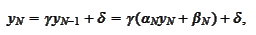
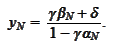Afterward, with
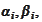
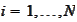already known we compute
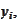with recursion in opposite direction
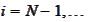according to the (
Factorization2
).
|
