e seek to improve efficiency of the finite difference scheme by splitting the
spacial operator
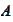into some positive components
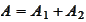and replacing the inversion of
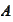with consecutive inversions of
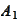and
.
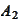In this section we always assume that some original scheme already has
stability and approximation properties and we show how to separate operator
while keeping these properties.
|
