ote that for any pair of operators
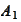 and
and
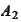 we can
write
we can
write
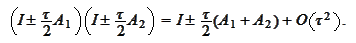 Hence, the
scheme
Hence, the
scheme
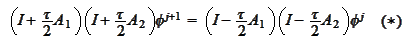 is equivalent to the
Crank-Nicolson
is equivalent to the
Crank-Nicolson
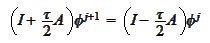 after grouping some
after grouping some
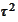 -order
terms. Therefore, if Crank-Nicolson approximates with second order then so
does the scheme (*).
-order
terms. Therefore, if Crank-Nicolson approximates with second order then so
does the scheme (*).
Claim
The scheme
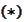 preserves stability.
preserves stability.
To transform the scheme (*) into a calculation recipe observe
that
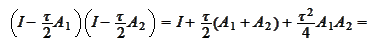
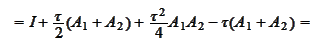
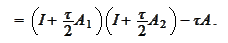 We
conclude
We
conclude
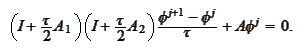 Hence, we replaced inversion of
Hence, we replaced inversion of
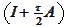 with consecutive inversions
with consecutive inversions
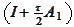 and
and
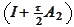 .
.
|