he purpose of this
section is to compute some basic probabilities associated with Poisson
process. Let
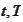be time moments,
.
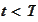The
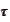denotes the time of the first jump. We subdivide the interval
![$\left[ t,T\right] $](graphics/notesCF__0__814.gif)
into
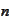small sub-intervals and let the size of each subinterval go to zero with
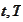being constants. We use the result
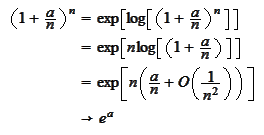as
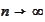and for
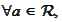and the notation
,
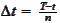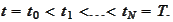Observe
that
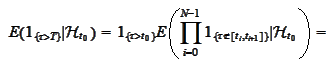We apply the
(
Chain_rule
):
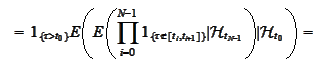From point of view of
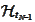the events
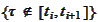are deterministic for
,
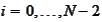hence,
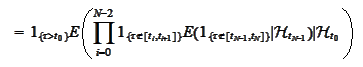then, by (
Poisson property
1
),
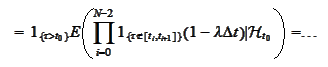We continue in similar manner and take a
limit:
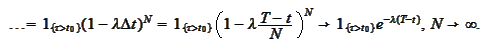
Therefore, with use of the formula
(
Poisson property 1a
), we
conclude
|
|
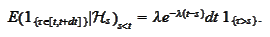
(Poisson property 2)
|
Similarly, for any integer
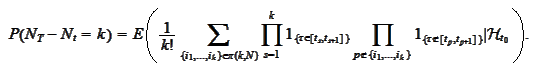where
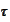denotes any jump of
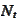and
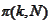denotes the set of permutations of
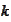integers from
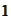to
.
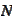The factorial exists because permutations of
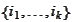constitute identical terms in the sum while the equality is based on
decomposition into disjoint events. We continue
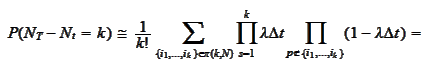
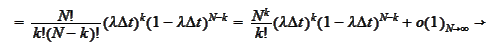We note
,
=
,
,
.
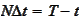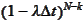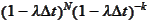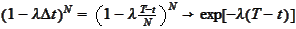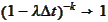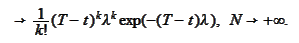Hence,
|
|
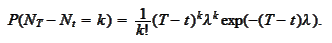
(Poisson property 3)
|
|
