he Heston equations are of the affine type. Hence, we proceed as discussed in
the section (
section about Affine
equation
).
We transform the equations to the
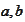 -form (
Affine equation
). Let
-form (
Affine equation
). Let
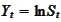 ,
,
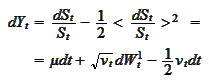
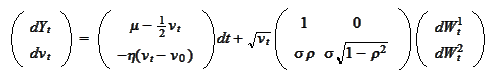 hence
hence
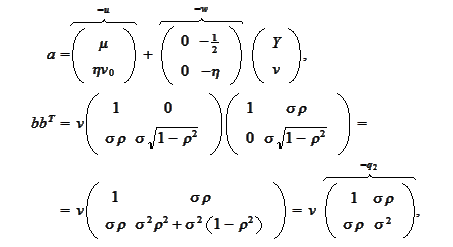 In
particular,
In
particular,
 According to the summary (
Affine
characteristic function 1
)-(
Affine
boundary conditions
) the
function
According to the summary (
Affine
characteristic function 1
)-(
Affine
boundary conditions
) the
function
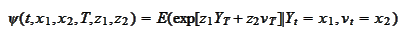 is given by the
expression
is given by the
expression
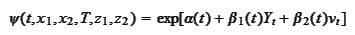 where the functions
where the functions
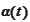 and
and
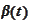 must satisfy the following system of
ODEs:
must satisfy the following system of
ODEs:
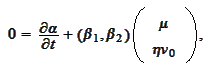
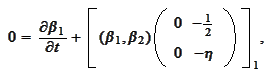
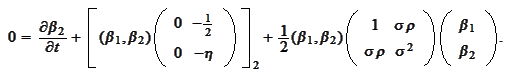 We transform the above
relationships:
We transform the above
relationships:
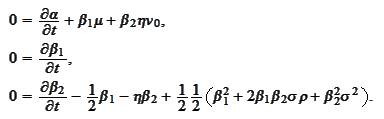 The
The
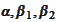 are to satisfy the final
conditions:
are to satisfy the final
conditions:
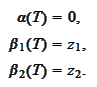 The next task is to solve the
equation
The next task is to solve the
equation
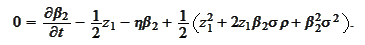 We introduce the convenience
notation
We introduce the convenience
notation
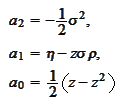 and
write
and
write
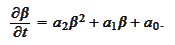 We perform the change of the unknown
function
We perform the change of the unknown
function
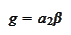 as
follows
as
follows
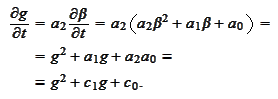 We perform the
transformation
We perform the
transformation
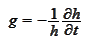 as follows:
as follows:
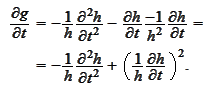 In
addition,
In
addition,
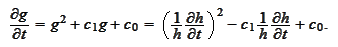 Hence,
Hence,
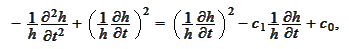 and,
consequently,
and,
consequently,
 We arrived to a linear equation. We look for solutions of the
form
We arrived to a linear equation. We look for solutions of the
form
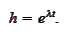 It suffices to
have
It suffices to
have
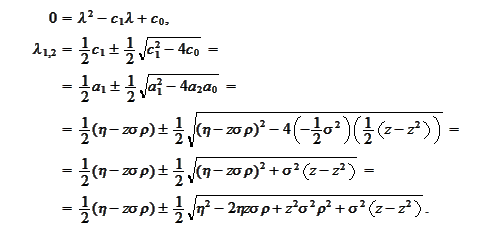 We mean to integrate over
We mean to integrate over
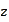 because this is the argument of the characteristic function and we want to
take the inverse Fourier or Laplace transform. Note that when
because this is the argument of the characteristic function and we want to
take the inverse Fourier or Laplace transform. Note that when
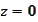 the expression under the square root is positive. For large
the expression under the square root is positive. For large
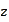 it is negative. Hence, we would rather change
it is negative. Hence, we would rather change
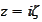 for real
for real
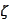 .
Then the square root is never zero. Indeed, the real part would be
.
Then the square root is never zero. Indeed, the real part would be
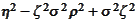 ,
where the correlation
,
where the correlation
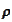 is not greater then 1.
is not greater then 1.
We perform the backward
substitutions
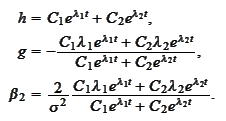 We introduce the quantity
We introduce the quantity
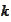 according to the relationship
according to the relationship
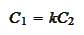 and transform the expression for
and transform the expression for
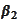
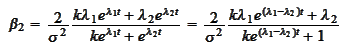 to emphasize that the requirement
to emphasize that the requirement
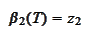 uniquely identifies the
uniquely identifies the
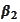 .
.
We now consider the equation for
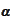 :
:
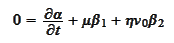 where the
where the
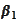 is a constant and the
is a constant and the
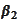 has just been
calculated:
has just been
calculated:
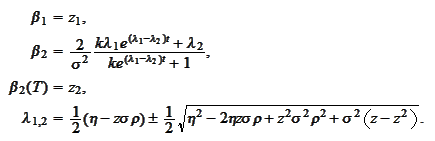 We
have
We
have
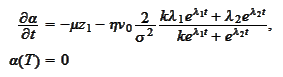 hence
hence
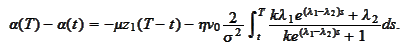 It remains to evaluate the
integral
It remains to evaluate the
integral
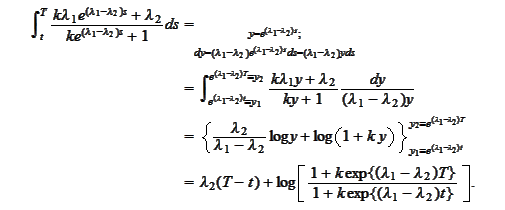 Since
Since
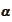 satisfies the final
condition
satisfies the final
condition
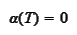 we
have
we
have
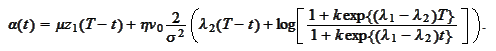
|