he reference is
[Xu]
.
Let
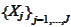 be a decomposition of
be a decomposition of
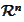 :
:
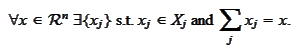 Let
Let
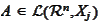 be a symmetric positive definite operator.
be a symmetric positive definite operator.
We define operators
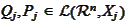 and
and
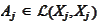 via the
relationships
via the
relationships
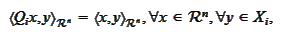
|
|
(Definition of Q i)
|
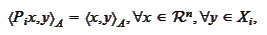
|
|
(Definition of P i)
|
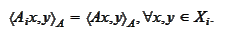
|
|
(Definition of A i)
|
For
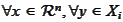 we
have
we
have
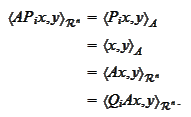 Thus
Thus
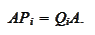
|
|
(Projection permuation)
|
Let
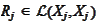 be a symmetric positive definite operator that (on motivational level) almost
inverts
be a symmetric positive definite operator that (on motivational level) almost
inverts
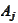 :
:
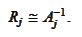 In context of the section
(
Preconditioning
) we introduce the
operator
In context of the section
(
Preconditioning
) we introduce the
operator
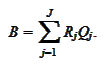
|
|
(Parallel subspace preconditioner)
|
We introduce the numbers
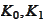 as follows.
as follows.
We introduce the notation
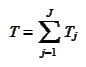 and
note
and
note
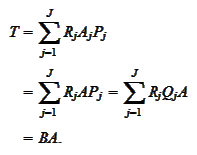
Definition
(Strengthened
Cauchy-Schwartz inequality) We define the matrix
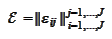 where
where
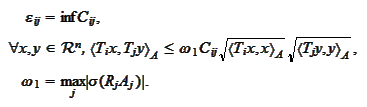
|
|
(Definition of Epsilon)
|
Proposition
(Magnitude of matrix Epsilon)
1.
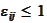 .
.
2. If
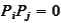 then
then
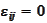 .
.
Proposition
(Estimate for K1 one)
1.
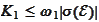 .
.
2.
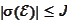 .
.
3. If
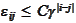 for some
for some
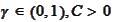 then
then
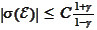 .
.
Proposition
(Estimate for K1 two) For any index set
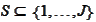 ,
,
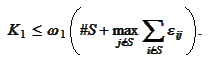
Proof
is tedious and straightforward.
|