unning procedure (
Conjugate gradients
)
for all
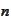 steps is not always feasible. In addition, numerical errors are likely to
destroy orthogonality of
steps is not always feasible. In addition, numerical errors are likely to
destroy orthogonality of
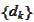 For these reasons it makes sense to study convergence of the procedure
(
Conjugate gradients
).
For these reasons it makes sense to study convergence of the procedure
(
Conjugate gradients
).
According to the formula
(
Conjugate gradient residue
selection
)
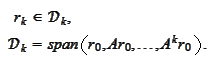 According to the formula (
Error and residual
2
) we then
have
According to the formula (
Error and residual
2
) we then
have
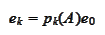 for some
for some
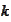 -th
degree polynomial
-th
degree polynomial
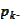 Furthermore, by tracing the recipe (
Conjugate
gradients
) directly we see that
Furthermore, by tracing the recipe (
Conjugate
gradients
) directly we see that
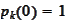 .
The conjugate gradient acts to minimize
.
The conjugate gradient acts to minimize
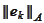 by manipulating coefficients of
by manipulating coefficients of
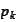 .
Thus, using notation of the definition
(
Positive definite inner
product
),
.
Thus, using notation of the definition
(
Positive definite inner
product
),
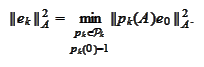 Since
Since
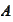 is a positive definite symmetric matrix, there exists a set of eigenvectors
is a positive definite symmetric matrix, there exists a set of eigenvectors
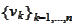 and positive eigenvalues
and positive eigenvalues
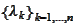 .
Then
.
Then
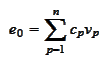 for some numbers
for some numbers
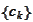 .
We
have
.
We
have
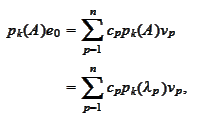
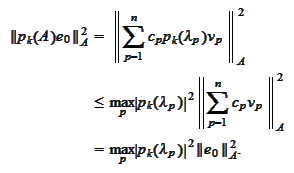 Therefore
Therefore
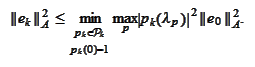 To evaluate the
To evaluate the
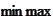 combination we aim to apply the proposition
(
Minimum norm
optimality of Chebyshev polynomials
). We are dealing with the minimization
over
combination we aim to apply the proposition
(
Minimum norm
optimality of Chebyshev polynomials
). We are dealing with the minimization
over
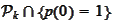 and the proposition is formed for
(
Minimum norm
optimality of Chebyshev polynomials
)
and the proposition is formed for
(
Minimum norm
optimality of Chebyshev polynomials
)
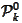 .
However, a review of the proof of that proposition shows that normalization is
irrelevant to the argument. We would still have optimality at a polynomial
that differ from a Chebyshev polynomial by multiplicative constant. We do,
however, need to transform from
.
However, a review of the proof of that proposition shows that normalization is
irrelevant to the argument. We would still have optimality at a polynomial
that differ from a Chebyshev polynomial by multiplicative constant. We do,
however, need to transform from
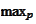 to
to
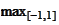 .
.
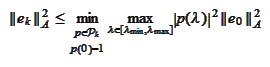 where
where
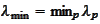 ,
,
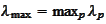 and
and
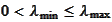 .
Next, we map
.
Next, we map
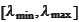 to
to
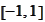 :
:
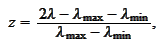
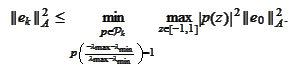 We now apply the proposition
(
Minimum norm
optimality of Chebyshev
polynomials
).
We now apply the proposition
(
Minimum norm
optimality of Chebyshev
polynomials
).
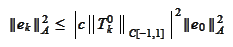 where the constant
where the constant
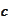 is the scale to
insure
is the scale to
insure
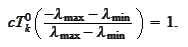 The
The
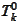 is a scale of
is a scale of
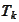 given
by
given
by
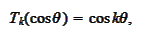 with the
consequences
with the
consequences
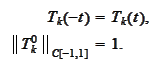 Hence, we
rewrite
Hence, we
rewrite
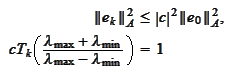 or, by taking square root and replacing
or, by taking square root and replacing
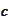 ,
,
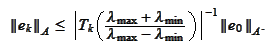 We introduce the quantity
We introduce the quantity
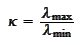
|
|
(Condition number)
|
then
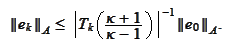 We use the proposition (
Chebyshev
polynomials
calculation
):
We use the proposition (
Chebyshev
polynomials
calculation
):
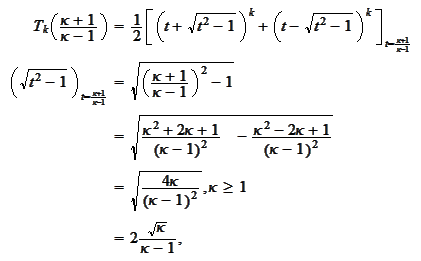
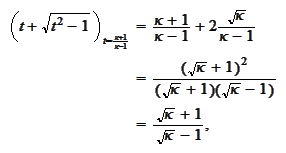
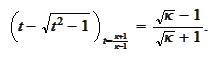 Therefore
Therefore
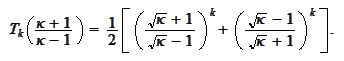 As
As
 grows the first term grows and the second term
vanishes.
grows the first term grows and the second term
vanishes.
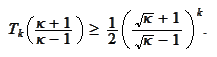 Then
Then
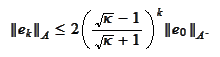
|