e build on results of the section
(
Change_of_measure_definition_section
).
Suppose
that
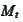is a numeraire with respect to the probability measure
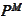and filtration
.
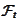By definition, this means that
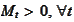and for any traded asset
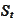the ratio
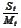is a
martingale:
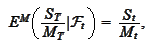with respect to some probability
.
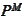We will refer to the positivity
condition
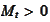as the "acceptable numeraire" condition. Suppose that
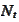is a price of another acceptable
(
)
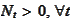instrument. We would like to produce a probability measure
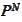such that for any traded asset
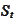
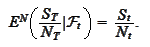We
write
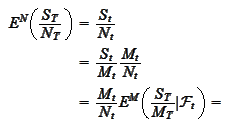
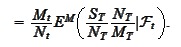Such transformation has the form
(
Main property of change of
measure
) with
.
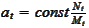To determine the constant we recall that
.
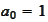Hence,
|
|
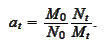
(Change of numeraire kernel)
|
|
