he code behind the LPoly class is based on calculations of the sections
(
Calculus behind the poly
module
) and
(
Calculus behind
the PiecewisePoly project
). There are, however, several differences
covered below.
We use the
notation
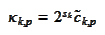
Proposition
(Conversion of representations) If
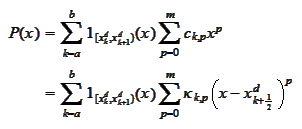 then
then
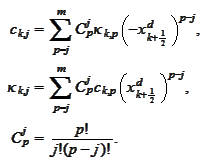
Proof
We
calculate
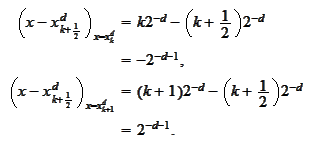
Proof
We
calculate
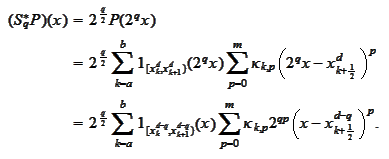
|