o understand the code of
the functions S(),T(), review the formulas
(
Property of scale and transport
1
)-(
Property of scale and
transport 7
).
The following propositions are reflected in the classes Poly and
PiecewisePoly.
Proposition
(Convolution of polynomials 2)
Let
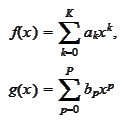 then
then
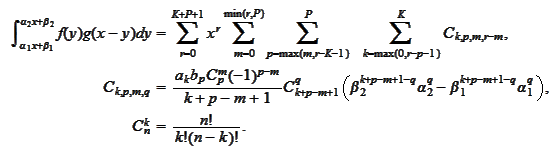
|