et
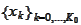 is a given array of numbers (integers or doubles). We would like to calculate
an array
is a given array of numbers (integers or doubles). We would like to calculate
an array
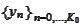 s.t.
s.t.
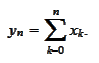
The presented procedure has
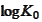 -proportional
processing time under assumption of infinite parallel processing capability.
-proportional
processing time under assumption of infinite parallel processing capability.
We proceed as follows. Choose an integer
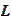 :
:
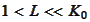 .
.
For step 0, we calculate in parallel
(
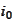 is the thread
index):
is the thread
index):
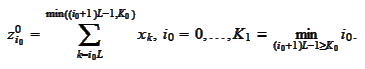
For step 1, we
calculate
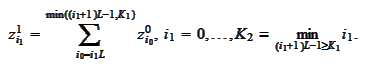
We continue, for step
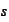 ,
we
calculate
,
we
calculate
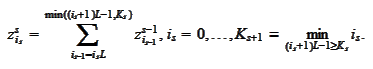
Summation in parallel for
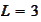 and
and
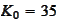 .
.
|
The last step would be
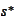 when
when
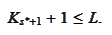
We
have
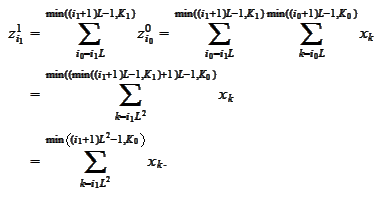 Similarly,
Similarly,
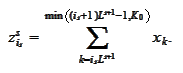 Note that for each
Note that for each
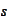
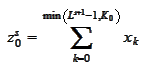 is a partial sum. Next, we correct the rest of the numbers.
is a partial sum. Next, we correct the rest of the numbers.
For step 0 we calculate (on a single
thread):
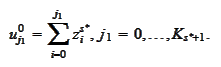 Thus,
Thus,
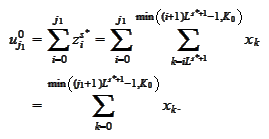 Note that the final
Note that the final
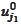 contains the final partial sum. Hence, there is no need to increment this
position anymore. This fact is reflected in slightly different indexing for
the following steps.
contains the final partial sum. Hence, there is no need to increment this
position anymore. This fact is reflected in slightly different indexing for
the following steps.
For step 1 we calculate (on
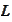 threads,
threads,
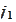 is the thread
index):
is the thread
index):
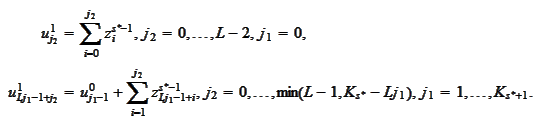 We adopt the
convention
We adopt the
convention
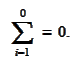 The index
The index
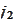 varies from 0 to
varies from 0 to
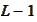 except for the boundary where
except for the boundary where
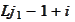 cannot
exceed or be equal to
cannot
exceed or be equal to
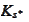 (because
indexes of
(because
indexes of
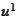 are in the same range as indexes of
are in the same range as indexes of
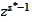 ):
):
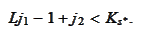 Hence, the stated range for
Hence, the stated range for
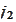 follows.
follows.
We
have
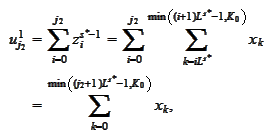
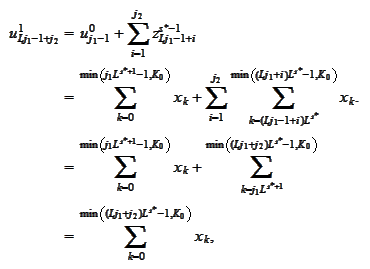 thus
thus
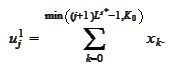
For general step
 we calculate (on
we calculate (on
 threads,
threads,
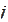 is the thread
index):
is the thread
index):
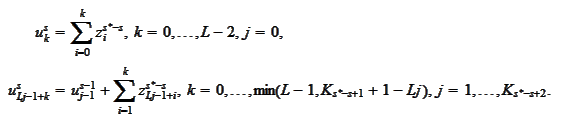 Assuming
that
Assuming
that
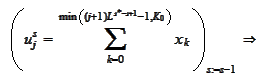
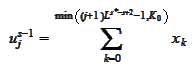 we
get
we
get
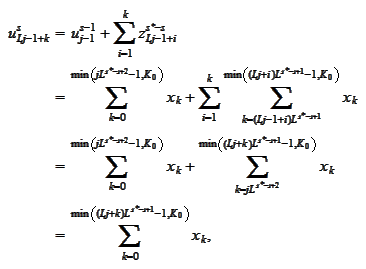 thus
thus
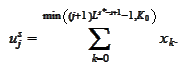
At
 we have the partial sums.
we have the partial sums.
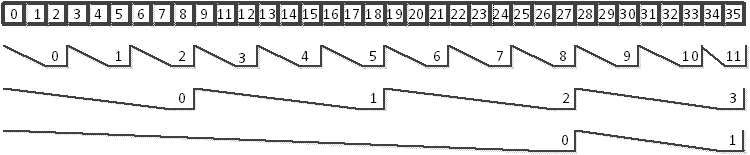
It remains to describe memory allocation and positioning for the intermediate
data
 and
and
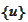 .
We place (see the figure (
Partial
summation in
parallel
))
.
We place (see the figure (
Partial
summation in
parallel
))
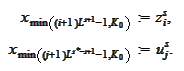
|