e introduce sets
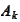and separate our sampling of
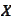into
:
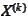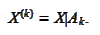Let
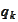be allocation rates,
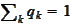and
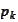be probabilities of
:
.
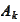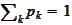We proceed with identification of parameters. We want to keep estimation
unbiased and reduce variance.
First, we seek weights
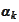such
that
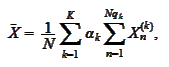
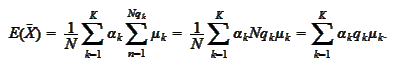
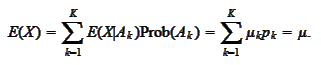Hence, we need to take
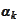so
that
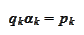to have an unbiased estimate.
We calculate the variance as
follows
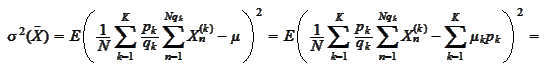
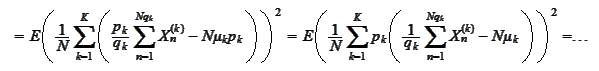
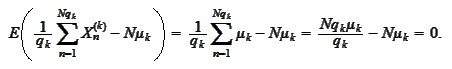
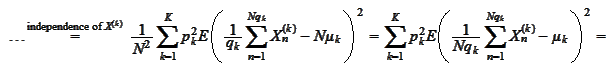
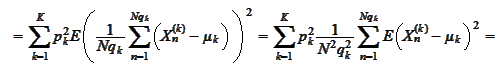
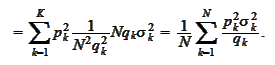
It remains to calculate two claims:
1. In case
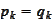we have
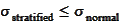(follows from formula (
Jensen inequality
)).
2. Optimal
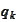is
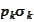up to normalization constant (direct verification).
|
