e wish to
find
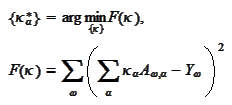where the
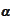and
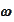are integer indexes
,
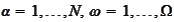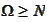and
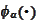is the indexed family of functions. This problem originates from the described
in the previous section stochastic optimization procedure. We perform the
standard
minimization:
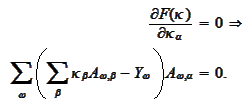The last equation simplifies to the matrix
problem
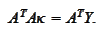At this point we invoke the Singular Value Decomposition, see
[Numerical]
. There exist matrices
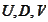such
that
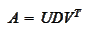and
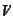is a square orthogonal matrix,
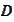is a diagonal matrix and
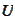is a matrix with orthogonal columns.
Consequently,
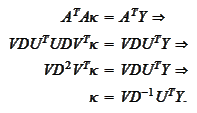Given the fact that the minimization problem is quadratic the last expression
is the solution.
The above procedure breaks if the matrix A does not have a full rank.
|
