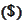Proof
We introduce a mapping
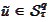 with the following
properties:
with the following
properties:
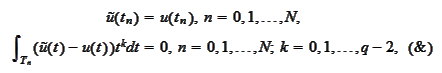 thus, for each
thus, for each
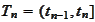 the
the
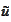 equals
equals
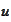 at
at
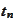 but does not equal
but does not equal
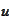 at
at
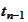 .
We proceed to prove existence and uniqueness of such
.
We proceed to prove existence and uniqueness of such
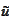 .
Let
.
Let
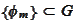 be an orthonormal basis of
be an orthonormal basis of
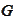 and
and
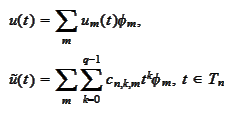 for some sequence
for some sequence
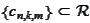 .
For every fixed
.
For every fixed
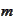 and
and
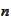 we need
we need
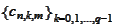 to
satisfy
to
satisfy
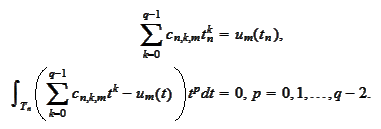 Thus, for each fixed
Thus, for each fixed
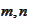 we have
we have
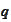 equations for
equations for
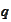 unknowns
unknowns
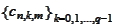 .
To complete the proof of existence of
.
To complete the proof of existence of
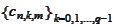 it remains to show that the homogenous system of
equations
it remains to show that the homogenous system of
equations
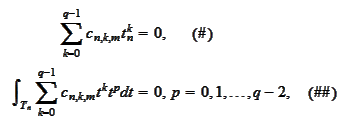 has only the trivial solution. Let
has only the trivial solution. Let
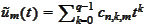 then, by
then, by
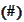 ,
,
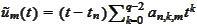 for some
for some
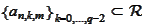 and, by
and, by
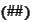 ,
,
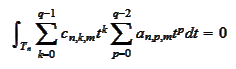 but
also
but
also
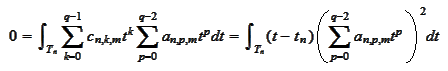 and both the terms
and both the terms
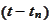 and
and
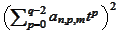 do not change sign on
do not change sign on
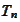 .
Thus, we must have
.
Thus, we must have
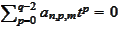 on
on
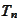 .
Existence of
.
Existence of
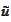 has been established.
has been established.
It follows from such result that if
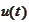 is a
is a
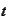 -polynomial
of degree
-polynomial
of degree
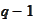 then
then
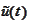 would approximate it exactly.
would approximate it exactly.
According to the proposition
(
Integral form of Taylor
decomposition
), for a function
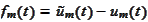 we
have
we
have
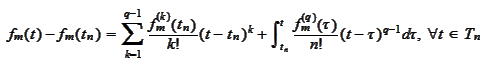 where
where
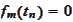 .
By polynomial approximation up to degree
.
By polynomial approximation up to degree
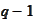 ,
we must
have
,
we must
have
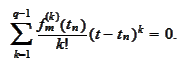 Indeed, if one of the derivatives
Indeed, if one of the derivatives
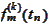 is not zero then we cannot have the polynomial approximation with the same
formula.
Thus
is not zero then we cannot have the polynomial approximation with the same
formula.
Thus
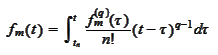 where
where
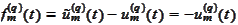 or
or
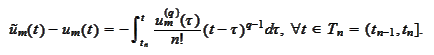 Consequently
Consequently
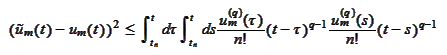 We use the formula (
Cauchy
inequality
),
We use the formula (
Cauchy
inequality
),
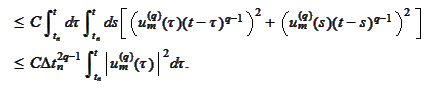 Then, by orthogonality of
Then, by orthogonality of
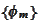 ,
,
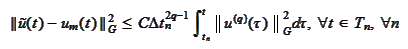 and by properties of the operator
and by properties of the operator
 listed in the condition (
Generic
parabolic PDE
setup
),
listed in the condition (
Generic
parabolic PDE
setup
),
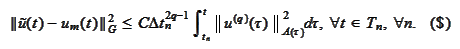
For
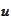 being a solution of the problem
(
Generic parabolic PDE problem
),
being a solution of the problem
(
Generic parabolic PDE problem
),
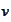 be a solution of the problem
(
Discontinuous Galerkin
time-discretization
) and
be a solution of the problem
(
Discontinuous Galerkin
time-discretization
) and
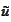 being the polynomial approximation defined in
being the polynomial approximation defined in
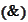 we decompose the error
we decompose the error
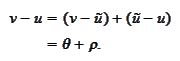 We already have the desired estimate for
We already have the desired estimate for
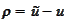 .
It remains to estimate
.
It remains to estimate
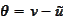 .
Note that both
.
Note that both
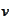 and
and
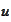 are solutions of the equation of the problem
(
Discontinuous Galerkin
time-discretization
), hence, for
are solutions of the equation of the problem
(
Discontinuous Galerkin
time-discretization
), hence, for
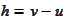 we
have
we
have
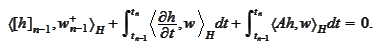 Consequently
Consequently
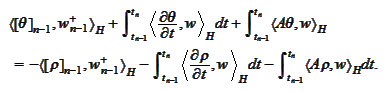 We calculate the
part
We calculate the
part
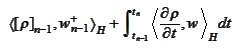 By definition of
By definition of
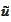 there is orthogonality of
there is orthogonality of
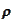 to
to
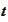 -variable
polynomials up to degree
-variable
polynomials up to degree
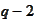 .
Thus, we perform integration by
parts.
.
Thus, we perform integration by
parts.
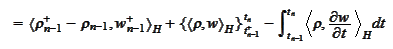 Now the integral is zero by the orthogonality because
Now the integral is zero by the orthogonality because
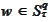 thus
thus
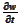 is a
is a
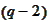 -degree
-degree
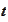 -variable
polynomial.
-variable
polynomial.
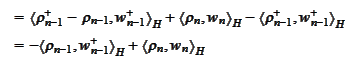 The
The
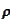 is zero at
is zero at
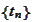 by definition of
by definition of
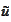 .
.
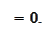
Therefore, we arrived
to
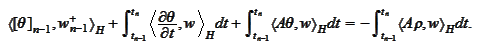 We set
We set
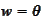 and evaluate the
part
and evaluate the
part
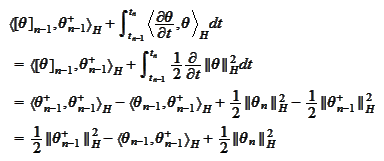 We use the formula (
Cauchy
inequality
).
We use the formula (
Cauchy
inequality
).
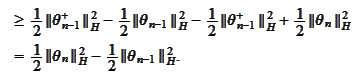 We arrived
to
We arrived
to
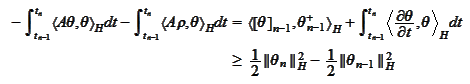 or
or
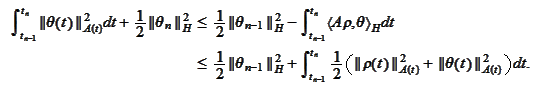 Hence
Hence
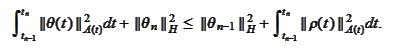 Thus
Thus
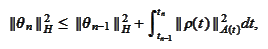
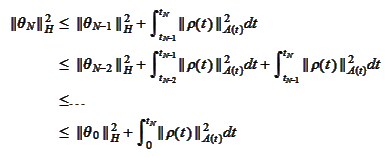 Note that
Note that
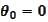 by definition of the components and
by definition of the components and
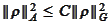 .
.
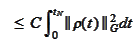 and we use the estimate
and we use the estimate