emoving time dependency via change of variables is not possible in general.
However, the special cases are of practical importance.
We consider the generic PDE of the
form
|
|
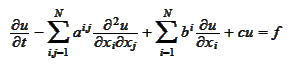
(Generic parabolic PDE)
|
where the functions
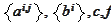are dependent on time
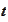and spacial variable
.
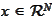In the following sections we calculate some generic changes of variables to
help to identify some special situations when the time dependency may be
removed from the functions
.
|
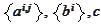