e have description of market under some numeraire
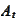 in
in
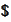 -denomination
and we would like to change to some
-denomination
and we would like to change to some
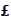 -denominated
numeraire
-denominated
numeraire
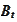 (The
(The
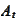 is measured in
is measured in
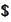 and the
and the
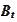 is measured in
is measured in
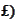 .
We introduce pound price of a dollar
.
We introduce pound price of a dollar
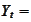
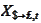 .
A
.
A
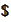 -amount
should be multiplied by
-amount
should be multiplied by
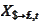 to obtain a
to obtain a
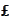 -amount.
We also introduce the reciprocal quantity
-amount.
We also introduce the reciprocal quantity
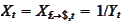 .
.
We proceed to calculate the drift of
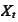 .
Suppose we have one pound at time
.
Suppose we have one pound at time
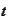 .
We may invest into pound bonds
.
We may invest into pound bonds
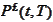 and convert to dollars at maturity. We may also convert to dollars right away
and invest into dollar bonds
and convert to dollars at maturity. We may also convert to dollars right away
and invest into dollar bonds
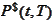 .
We get a dollar outcome in both situations and the dollar risk neutral
expectation of both strategies should be the same. We express such conclusion
below:
.
We get a dollar outcome in both situations and the dollar risk neutral
expectation of both strategies should be the same. We express such conclusion
below:
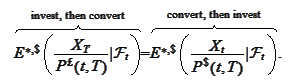 We move the time
We move the time
 -known
quantities out of the expectation sign and
obtain
-known
quantities out of the expectation sign and
obtain
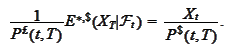 Let
Let
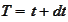 .
We
get
.
We
get
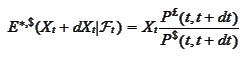 and
consequently
and
consequently
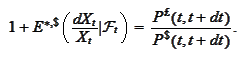 Note that the expectation
Note that the expectation
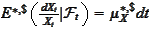 is the drift that we are calculating and the bonds have
expansions
is the drift that we are calculating and the bonds have
expansions
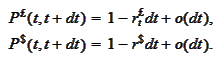 The above is to be compared with the formula (
Bond
SDE
) under the condition
The above is to be compared with the formula (
Bond
SDE
) under the condition
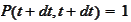 .
Hence,
.
Hence,
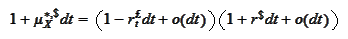 or
or
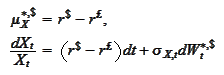 where the
where the
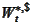 is standard Brownian motion with respect to risk neutral probability measure
on dollar market. The result agrees with the intuition that when the dollar
MMA rate is higher than the pound MMA rate then the exchange rate should drift
against dollar (otherwise there would be arbitrage).
is standard Brownian motion with respect to risk neutral probability measure
on dollar market. The result agrees with the intuition that when the dollar
MMA rate is higher than the pound MMA rate then the exchange rate should drift
against dollar (otherwise there would be arbitrage).
By similar
argument
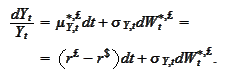 We also
have
We also
have
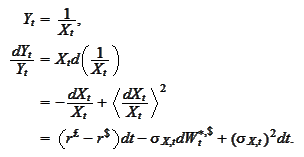 Hence,
Hence,
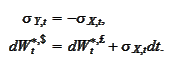
|
|
(X to Y connection)
|
We now collect results for general case. We want to change numeraire from
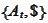 to
to
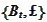 ,
where
,
where
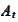 is a price of a traded asset denominated in
is a price of a traded asset denominated in
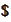 .
We execute the
program
.
We execute the
program
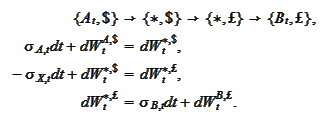 Hence,
Hence,
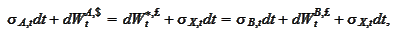 or
or
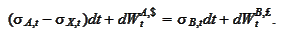
|