e start
from the problem
(
Backward
discontinuous Galerkin time-discretization
): We seek
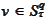 such that for every
such that for every
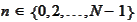 and any
and any
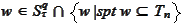 ,
,
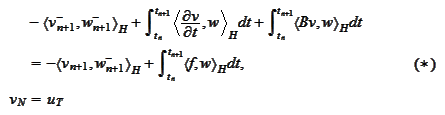 where
where
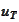 is input data. By inclusion
is input data. By inclusion
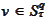 ,
the function
,
the function
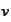 has the
form
has the
form
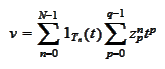 The functions
The functions
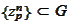 are sought as linear combinations of a wavelet
basis:
are sought as linear combinations of a wavelet
basis:
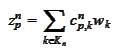 for some finite index set
for some finite index set
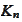 .
A system of linear equations is obtained by
selecting
.
A system of linear equations is obtained by
selecting
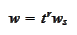 for all
for all
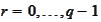 and all
and all
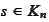 .
.
We substitute definitions into
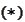 and
calculate
and
calculate
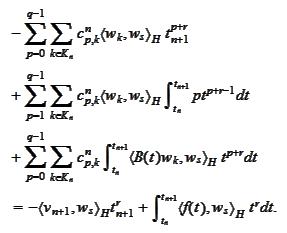
We treat the pairs
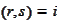 ,
,
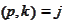 as a single indexes
as a single indexes
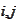 .
The above equation has the
form
.
The above equation has the
form
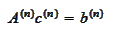 where
where
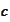 is a column
is a column
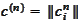 ,
,
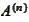 is a
matrix
is a
matrix
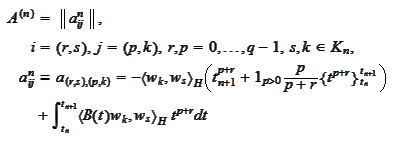
|
|
(Matrix of discontinuous Galerkin)
|
and the column
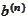 comes from previous step or input
data:
comes from previous step or input
data:
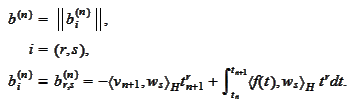
We will discover in the following sections that we can frequently do
successful calculations using
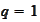 .
We adapt the formulas to such
case:
.
We adapt the formulas to such
case:
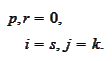 We
get
We
get
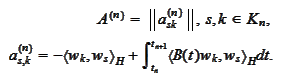 The column
The column
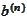 is
defined
is
defined
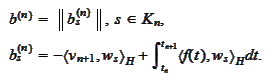 For
For
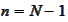 we
have
we
have
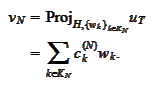 For
For
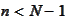 we use result of the previous
step
we use result of the previous
step
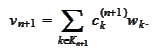 In either
case
In either
case
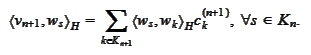
|