he matrixes
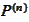and
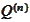off the section
(
Reduction
to system of linear algebraic equations for mean reverting equation
) may
be evaluated by the standard means provided by the library of the section
(
Manipulation
of localized piecewise polynomial functions
). However, the matrix
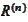requires a custom Cuda coding. We perform the task in this section.
We need code for evaluation of the
integral
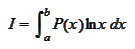where
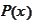was introduced in the section
(
Manipulation
of localized piecewise polynomial
functions
):
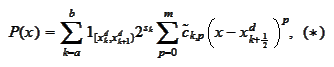
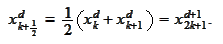
We
calculate
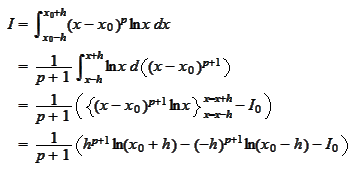
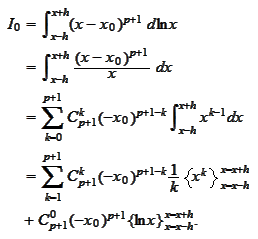We have a problem if
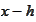is zero. In addition, we defeat the purpose of having a localized
representation to avoid subtracting large values. By doing so in present
situation we compound the problem. Therefore, we revert back to regular
representation for the function
:
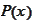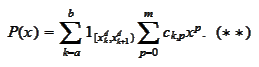We
evaluate
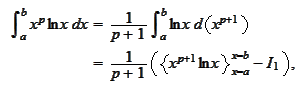
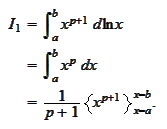In such case we can replace expressions
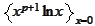with
zero:
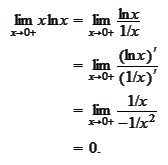
The implementation may be found in the project PiecewisePoly, function
Poly::logIntegral.
|
