e multiply the
equation
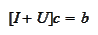 of the summary
(
Reduction
to system of linear algebraic equations for q=1
) with a diagonal matrix
of the summary
(
Reduction
to system of linear algebraic equations for q=1
) with a diagonal matrix
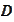 :
:
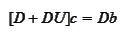 and transform the
matrix
and transform the
matrix
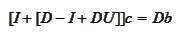 or
or
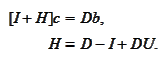 We would like to choose the matrix
We would like to choose the matrix
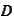 so that the Frobenius norm of the
matrix
so that the Frobenius norm of the
matrix
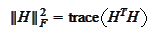 would be minimal.
would be minimal.
We
calculate
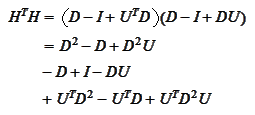 thus
thus
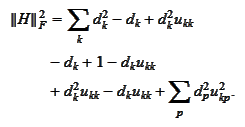 We observe that
We observe that
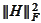 is a positive quadratic function of
is a positive quadratic function of
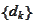 ,
thus the minimum is located where the derivatives
,
thus the minimum is located where the derivatives
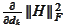 vanish. We
differentiate
vanish. We
differentiate
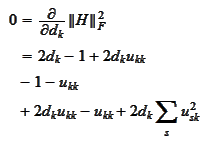 and
transform
and
transform
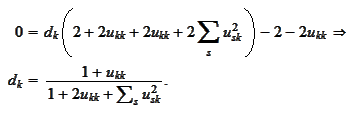
Calculation of the script blackDp.py in the directory
OTSProject/python/wavelet2 shows that such preconditioner is very effective.
For the parameters, set in the section
(
Example Black equation
parameters
) and
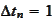 ,
the matrix
,
the matrix
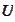 has the following
metrics:
has the following
metrics:
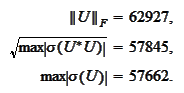 The matrix
The matrix
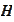 has the following
metrics:
has the following
metrics:
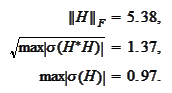 If
If
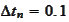 then the matrix
then the matrix
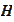 has the following
metrics:
has the following
metrics:
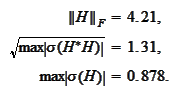 If
If
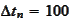 then the matrix
then the matrix
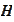 has the following
metrics:
has the following
metrics:
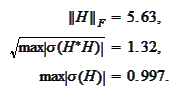 Note that even for
Note that even for
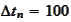 the spectral radius stays below
the spectral radius stays below
 .
In addition, the Frobenius norm
.
In addition, the Frobenius norm
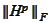 decreases if
decreases if
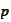 increases and the maximal singular value drops below 1 for reasonably large
increases and the maximal singular value drops below 1 for reasonably large
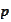 .
.
|