his section documents a negative result.
We would like to construct a preconditioner via exact inversion of the Black
PDE.
In the section
(
Asymptotic
expansion for Black equation
) we calculated solution for Black equation.
Let
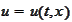be the solution of the
problem
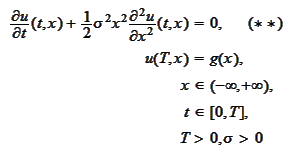for integrable function
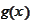then
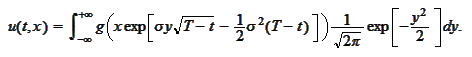We would like to put the expression into the
form
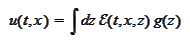for some kernel
.
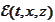We introduce the
notation
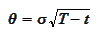then
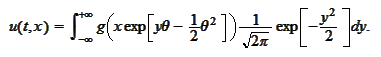We make the
change
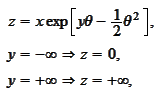
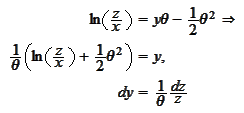then
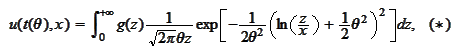
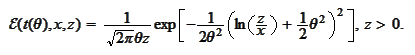
We introduce the projections of
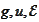on some basis
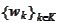and index set
.
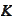We
approximate
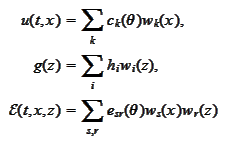then we apply the operation
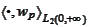to the equation
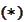and
obtain
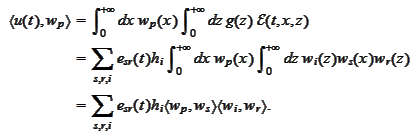Thus
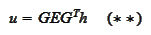where the
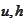are
columns
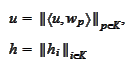and
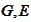are
matrixes
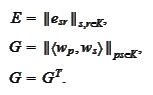
Note
that
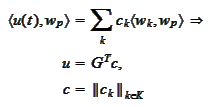and
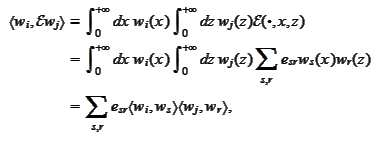
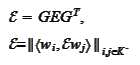It follows from
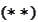
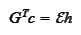or
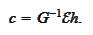We intend to use (some approximation of)
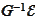as a preconditioner. We need some way to evaluate the integrals
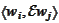perhaps with relaxed precision. The simplest road is to use crudification
operator to simplify piecewise polynomial representations of the basis
,
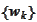make square of the number of pieces below 256 and then employ Cuda.
The functions
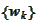are piecewise quadratic polynomials. Our next task is to calculate expressions
for the
integrals
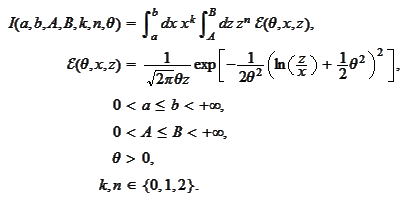We calculate the
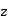-integral:
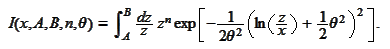We make the change
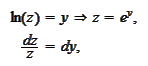
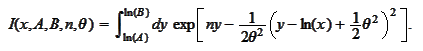We complete the
square:
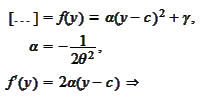
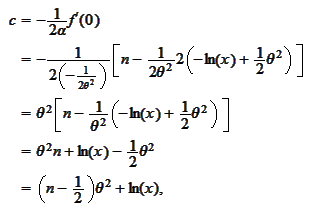
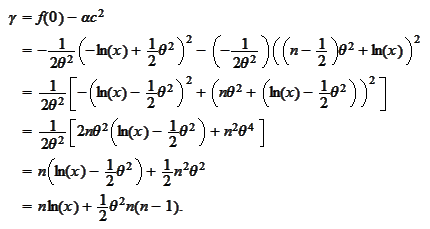Thus
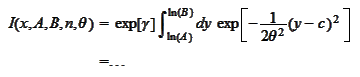We make the
change
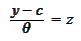
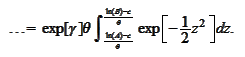
We cannot proceed with explicit evaluation of the
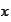-integral
from this point. Hence, we perform a linear approximation of the function
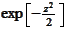on the interval of interest
:
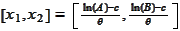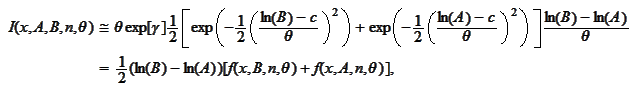
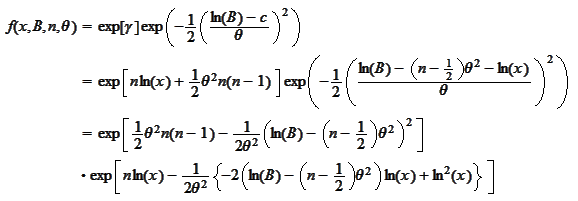
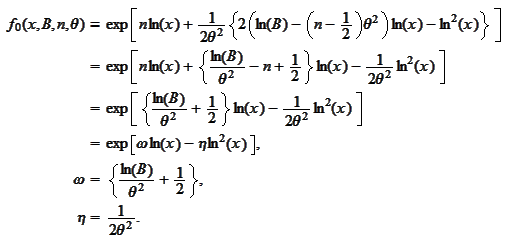
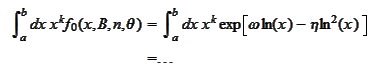Make the change
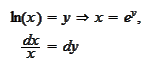then
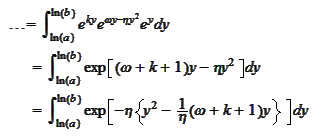We complete the
square:
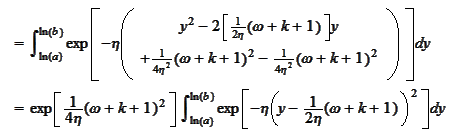and do linear
approximation
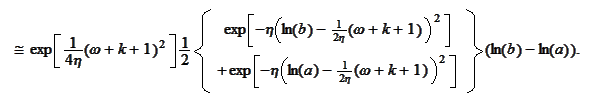
We put our results
together.
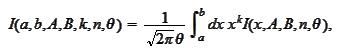
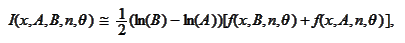
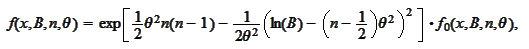
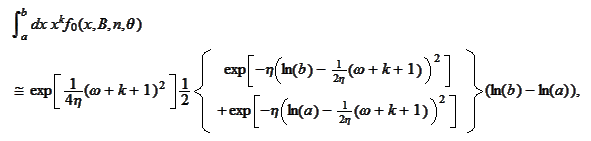
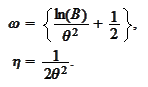
Due to lack of absolute precision and the number of required numerical
operations this approach does not offer improvement over combined application
of recipes of the sections
(
Diagonal preconditioner
) and
(
Reduction to well
conditioned form
). The author did not do a numerical experiment or
verification of the above summary.
|
