n the context of the section
(
Optimal stopping time
problem
) we consider the state
process
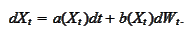The functions
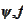are independent of time and
.
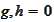It follows from the considerations of the sections
(
Representation
of solution for elliptic PDE using stochastic process
) and
(
Optimal stopping time
problem
) that the PDE of the problem is of the elliptic type.
|
