Proposition
(Boundedness of surjection) In context
of the condition (
Space splitting setup
)
and for a stable splitting, the operator
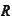 is bounded and
is bounded and
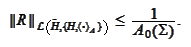
Proof
For any
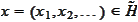 we
estimate
we
estimate
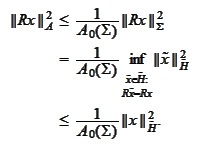
Proposition
(Boundedness of adjoint of
surjection) In context of the condition
(
Space splitting setup
) and for a stable
splitting, the operator
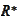 is bounded and
is bounded and
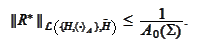
Proof
The symmetry follows from the proposition
(
Form of Schwarz operator
) and
generic properties of taking
adjoint:
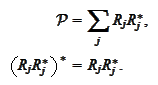
For any
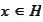 we introduce a class
we introduce a class
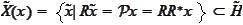 .
The class
.
The class
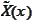 is never empty by surjectivity of
is never empty by surjectivity of
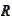 ,
see the condition (
Space splitting
setup
). Then, for any
,
see the condition (
Space splitting
setup
). Then, for any
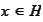 and
and
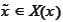 we
calculate
we
calculate
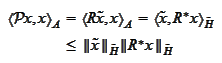 where the equality takes place for
where the equality takes place for
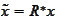 and
and
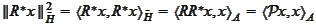 .
We
obtained
.
We
obtained
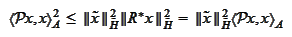 or
or
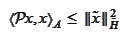 with equality reached at
with equality reached at
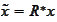 .
Thus
.
Thus
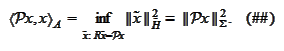 Next, we establish the upper bound for
Next, we establish the upper bound for
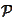 .
We calculate, using the stability of splitting and
.
We calculate, using the stability of splitting and
 ,
,
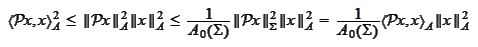 thus
thus
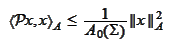 or
or
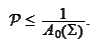
Next, we establish the lower bound for
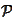 .
We use again the surjectivity of
.
We use again the surjectivity of
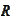 ,
see the condition (
Space splitting
setup
), to introduce a non empty class
,
see the condition (
Space splitting
setup
), to introduce a non empty class
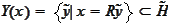 .
Then, for any
.
Then, for any
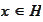 and any
and any
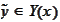
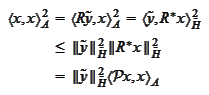 At this point we take infimum with respect to
At this point we take infimum with respect to
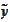 and use the definition of
and use the definition of
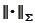 ,
,
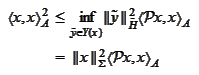 We use stability of
splitting,
We use stability of
splitting,
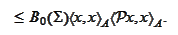 Thus
Thus
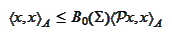 or
or
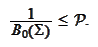 Therefore,
Therefore,
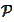 is invertible. The formula
is invertible. The formula
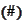 now follows from
now follows from
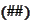 .
.
|