he following is the program of our
actions:
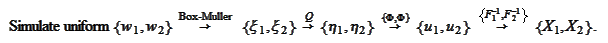 We start from the uniform on
We start from the uniform on
![$[0,1]$](graphics/notesCF__0__2352.gif) random variables
random variables
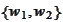 and apply the Box-Muller procedure, described in the claim
(
Box-Muller procedure
). The step
and apply the Box-Muller procedure, described in the claim
(
Box-Muller procedure
). The step
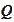 is a unitary linear transformation of the iid standard normal variables
is a unitary linear transformation of the iid standard normal variables
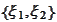 into a jointly normal variables
into a jointly normal variables
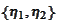 .
The transformation
.
The transformation
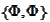 produces two correlated uniform variables according to the
(
Sklar_theorem_2
). The transformation
produces two correlated uniform variables according to the
(
Sklar_theorem_2
). The transformation
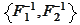 is the application of the (
Sklar_theorem_1
).
We spell out every step below.
is the application of the (
Sklar_theorem_1
).
We spell out every step below.
We choose the transformation
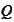 ,
,
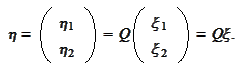 to construct the
to construct the
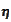 with the following
properties
with the following
properties
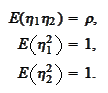 We observe
that
We observe
that
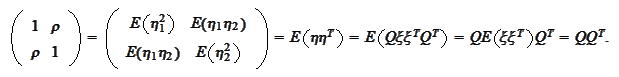 Hence, it suffices to chose
Hence, it suffices to chose
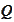 according
to
according
to
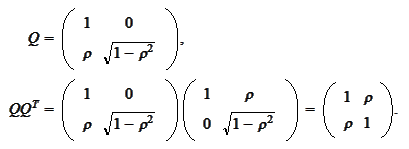
The step
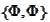 is performed according to the idea behind the result
(
Sklar_theorem_2
). We note that the cumulative
standard normal distribution
is performed according to the idea behind the result
(
Sklar_theorem_2
). We note that the cumulative
standard normal distribution
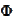 produces a uniform on [0,1] random variable
produces a uniform on [0,1] random variable
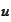 from a standard normal variable
from a standard normal variable
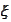 according to the rule
according to the rule
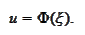 Indeed, for such
Indeed, for such
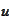 we calculate
we calculate
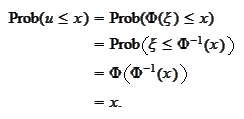
We also introduce the function
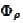 and uniform on [0,1] random variables
and uniform on [0,1] random variables
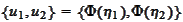 :
:
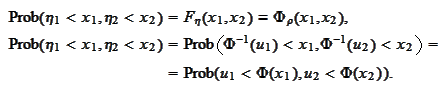 Hence,
Hence,
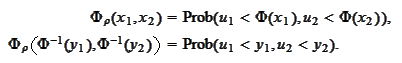
For the final step
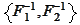 we are given the cumulative distributions
we are given the cumulative distributions
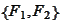 .
We simulate the variables
.
We simulate the variables
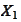 and
and
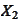 according to the
rules
according to the
rules
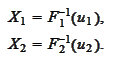 Such variables have marginal cumulative distributions
Such variables have marginal cumulative distributions
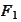 and
and
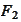 respectively. Their correlation is controlled by the parameter
respectively. Their correlation is controlled by the parameter
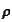 .
The joined distribution is given by the following
calculation:
.
The joined distribution is given by the following
calculation:
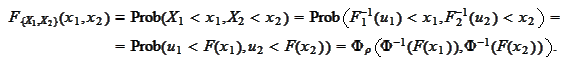 If
If
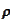 is 0 then the
is 0 then the
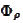 splits into product and the
splits into product and the
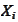 are uncorrelated. Preservation of sign of correlation takes place.
are uncorrelated. Preservation of sign of correlation takes place.
|