e consider the problem
(
Poisson
equation with Dirichlet boundary condition
).
Let
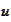 be a solution of the problem
(
Poisson
equation with Dirichlet boundary condition
). According to the proposition
(
Green formula
) and the boundary
conditions
be a solution of the problem
(
Poisson
equation with Dirichlet boundary condition
). According to the proposition
(
Green formula
) and the boundary
conditions
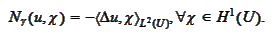
Condition
(Approximation in Nitsche norm) We
assume that the finite dimensional spaces
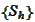 satisfy the following conditions
satisfy the following conditions
1.
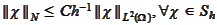 .
.
2.
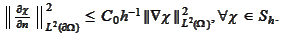
3.
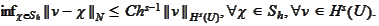
Problem
(Poisson equation weak
formulation 2) Find the solution
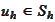 that satisfies the condition
that satisfies the condition
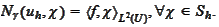
Note
that
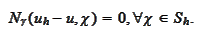
|