collection
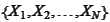of independent and identically distributed (iid) random variables with
distribution
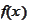is called a random sample from population
.
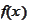Let
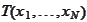be a real valued function whose domain includes the sample space of
.
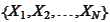The random variable
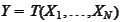is called "statistic".
Sample mean and variance are
,
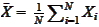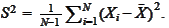
The following identity is
useful
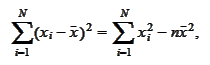for any numbers
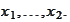
For any sample
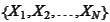of population with mean
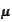and finite variance
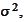the sample mean and variance have the properties
.
|
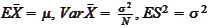