t remains to describe a recipe for construction of the maps
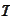 ,
,
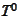 ,
,
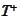 .
.
The map
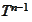 indexes a matrix. We choose the "row-by-row" indexing.
If
indexes a matrix. We choose the "row-by-row" indexing.
If
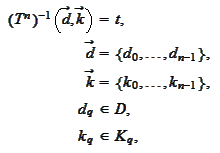 then
then
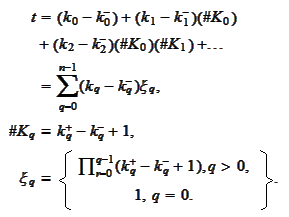 Therefore,
if
Therefore,
if
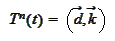 then
then
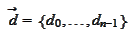 and
and
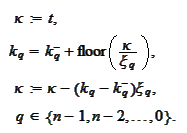
With
 so defined we can calculate the
arrays
so defined we can calculate the
arrays
 in parallel.
in parallel.
Therefore, to identify the mappings
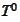 and
and
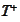 it suffices to map domains of these mappings into the domain of
it suffices to map domains of these mappings into the domain of
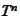 .
For each
.
For each
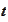 from domain of
from domain of
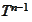 we perform on a separate thread the following
calculation:
we perform on a separate thread the following
calculation:
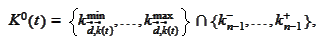
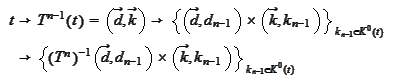 where the last set is the set of numbers in domain of
where the last set is the set of numbers in domain of
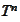 .
The total size of calculated data is known apriori after the arrays
.
The total size of calculated data is known apriori after the arrays
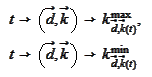 have been calculated. Hence, after we calculate each
have been calculated. Hence, after we calculate each
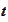 on a separate thread, we do not need to merge data because the collection can
happen directly into correct place.
on a separate thread, we do not need to merge data because the collection can
happen directly into correct place.
To be precise,
let
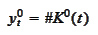 and
and
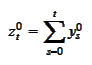 is obtained via the procedure of the section
(
Calculation of
partial sums in parallel
). We allocate an
array
is obtained via the procedure of the section
(
Calculation of
partial sums in parallel
). We allocate an
array
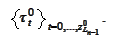 For every
For every
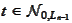 (thread index) we
calculate
(thread index) we
calculate
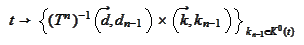 as described above. We allocate the result into
as described above. We allocate the result into
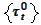 as follows. For
as follows. For
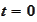 the result is placed
into
the result is placed
into
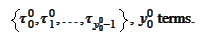 For
For
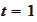 the result is placed
into
the result is placed
into
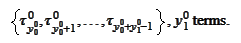 For any
For any
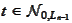 the result is placed
into
the result is placed
into
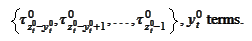 The result
The result
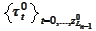 is the indexing of the boundary subdomains
and
is the indexing of the boundary subdomains
and
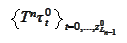 is enumeration of the boundary subdomains.
is enumeration of the boundary subdomains.
The
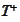 case is almost identical. We replace
case is almost identical. We replace
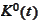 with
with
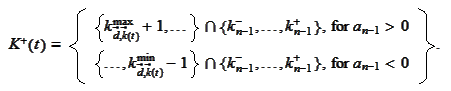 Indeed, we are interested in the
area
Indeed, we are interested in the
area
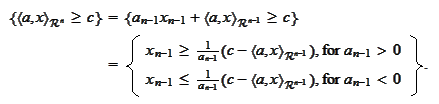 We arrive to the following
procedure.
We arrive to the following
procedure.
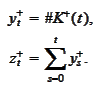 Allocate
Allocate
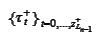 and, for every
and, for every
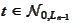 ,
place result
of
,
place result
of
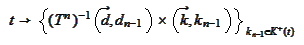 into
into
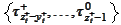 .
Then
.
Then
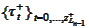 is the indexing of the internal subdomains
and
is the indexing of the internal subdomains
and
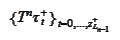 is enumeration of the internal subdomains.
is enumeration of the internal subdomains.
|