ypically, in financial applications, the final payoff function depends on a
small subset of variables
:
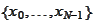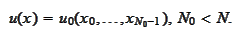We represent such situation
as
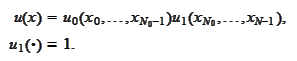Thus
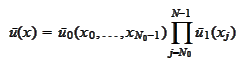where the function
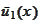is the projection of
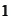on
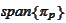in one dimension.
Assuming
that
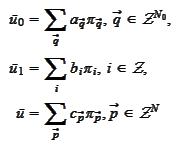we
get
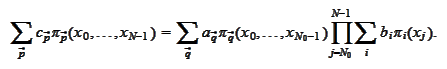We denote
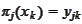then
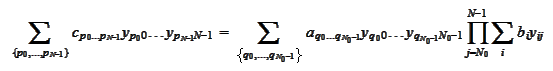thus
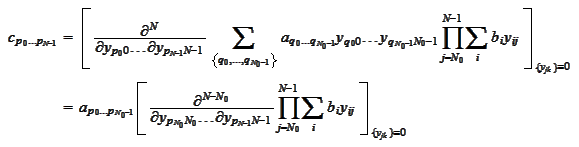Note that for every derivative
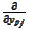there is exactly one term in the product that has dependency on the variable
.
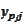We
continue:
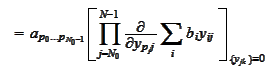The
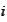-sum
is a basis decomposition. Hence, there is always an
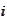in the sum such that
.
|
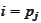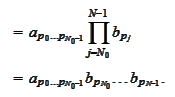
