n this section
we use the crudification operator, see the definition
(
Crudification operator
), to implement
the properties (
Wavelet approximation
2
)-(
Wavelet approximation 4
) with
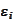close to machine precision and wavelet representations of reasonable size. We
look at
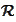-based
scaling function basis
.
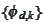The script wavelet2\_run_cascade.py performs the following procedure.
For the PiecewisePoly library (see the section
(
Piecewise polynomials in
parallel
)) compiled over double precision and
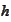calculated for
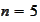we
obtain
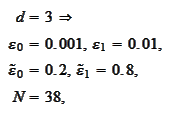
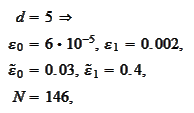
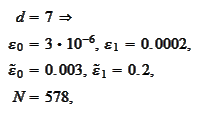
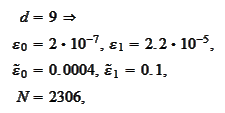
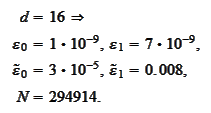
The script wavelet2\approxTest.py calculates the
.
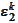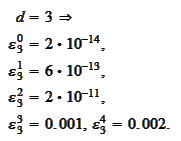
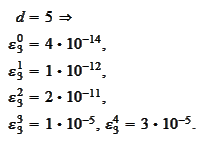
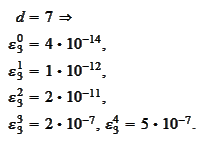
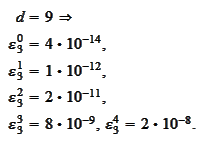
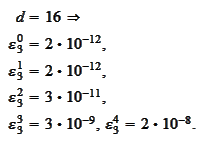
The same procedure is implemented in the scripts _l_run_cascade.py and
l_approxTest.py using the class LPoly introduced in the section
(
Manipulation
of localized piecewise polynomial functions
). The convergence results are
as
follows.
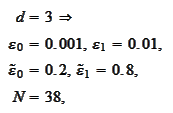
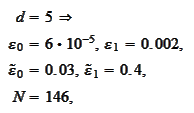
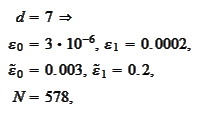
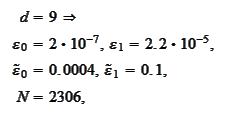
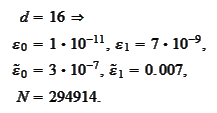Thus, there is a significant improvement in
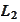approximation for high
.
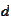The
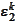results are as
follows.
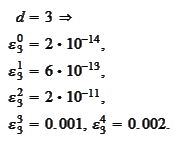
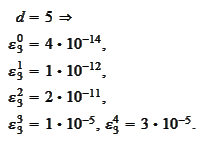
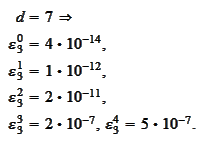
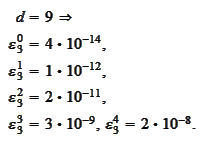
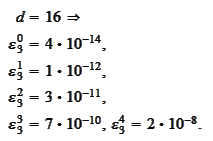Thus, improvement in polynomial approximation is relatively slight.
|
