dapting
scaling functions to the interval [0,1] is based on the technique of the
section (
Adapting GMRA to
interval [0,1]
). The python code is located in the file
"OTSProjects\python\wavelet\interval\interval.py".
The class PhiGenerator performs the task. The notation in the code follows the
notation of the section
(
Adapting GMRA to interval
[0,1]
). The example of use may be found in the function "makePhiGen" in
the file "_run_interval.py". The same file performs various direct
verifications of correctness of the procedure.
Examination of the code in the file interval.py reveals that we slightly
deviate from the procedure of the section
(
Adapting GMRA to interval
[0,1]
). The reason is numerical stability. The procedure is based on the
scaling functions
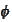 ,
,
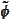 that come from infinite cascade procedure. We have to stop the cascade
procedure at some limited number of steps. As a result, we do not get exact
biorthogonality of the translation bases around
that come from infinite cascade procedure. We have to stop the cascade
procedure at some limited number of steps. As a result, we do not get exact
biorthogonality of the translation bases around
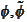 .
The biorthogonality is essential for the procedure of the section
(
Adapting GMRA to interval
[0,1]
). Without it we do not get biorthogonality between internal and
boundary scaling functions. If we start with a slight deviation from
biorthogonality of
.
The biorthogonality is essential for the procedure of the section
(
Adapting GMRA to interval
[0,1]
). Without it we do not get biorthogonality between internal and
boundary scaling functions. If we start with a slight deviation from
biorthogonality of
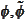 then the error is amplified when we multiply by the matrixes
then the error is amplified when we multiply by the matrixes
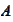 and
and
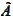 .
To see this, calculate eigenvalues for the matrixes
.
To see this, calculate eigenvalues for the matrixes
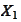 and
and
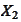 .
For symmetric biorthogonal scaling functions, calculated directly from the
procedure of the section
(
Adapting GMRA to interval
[0,1]
) and
.
For symmetric biorthogonal scaling functions, calculated directly from the
procedure of the section
(
Adapting GMRA to interval
[0,1]
) and
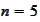 (the smallest, simplest case), the 5 eigenvalues range from 2.5e-1 to 2.0e-11.
This is the origin of numerical troubles that follow after that. On the other
hand, achieving biorthogonality of
(the smallest, simplest case), the 5 eigenvalues range from 2.5e-1 to 2.0e-11.
This is the origin of numerical troubles that follow after that. On the other
hand, achieving biorthogonality of
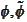 with great precision is costly.
with great precision is costly.
The difficulty originates in the approximation properties of the system
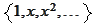 that we use when constructing the initial boundary functions
that we use when constructing the initial boundary functions
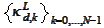 ,
,
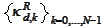 ,
,
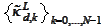 ,
,
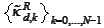 .
As we increase the maximal degree, the condition number of Gram matrix
increases. To remove the difficulty, we rotate the system
.
As we increase the maximal degree, the condition number of Gram matrix
increases. To remove the difficulty, we rotate the system
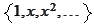 into shifted Legendre polynomials. Indeed, the matrix
into shifted Legendre polynomials. Indeed, the matrix
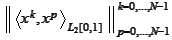 has eigenvalues in the range from 1.5 to 3.3e-6 for
has eigenvalues in the range from 1.5 to 3.3e-6 for
 (see the script tPwrOrt.py) but the same matrix for the Legendre polynomials
is equal to
(see the script tPwrOrt.py) but the same matrix for the Legendre polynomials
is equal to
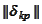 .
.
The more efficient solution is obtained by performing orthogonalization of
polynomials
 with custom scalar
product:
with custom scalar
product:
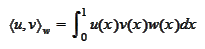 for some positive on
for some positive on
![$\left[ 0,1\right] $](graphics/notesCF__2__168.gif) function
function
 .
Indeed, our concern is preserving biorthogonality of
.
Indeed, our concern is preserving biorthogonality of
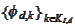 vs
vs
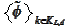 (biorthogonality across the boundary index
(biorthogonality across the boundary index
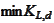 ,
and similarly on the right side). We expect one of the quantities
,
and similarly on the right side). We expect one of the quantities
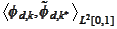 ,
,
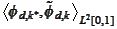 ,
,
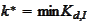 ,
,
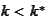 to deviate the most from zero. Therefore, we obtain good stability if we
select
to deviate the most from zero. Therefore, we obtain good stability if we
select
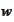 from
from
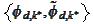 .
Experimentation shows (see the classes CondNumberMinimizer and
PolynomialMinimizer and the script _run_interval.py) that optimization of
.
Experimentation shows (see the classes CondNumberMinimizer and
PolynomialMinimizer and the script _run_interval.py) that optimization of
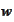 does not provide significant improvement over such recipe.
does not provide significant improvement over such recipe.
In addition, we use the Python module "decimal" to control numerical
precision.
With these two modifications in place, it is possible to achieve
precision
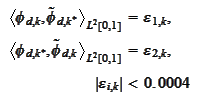 for 8 steps of cascading procedure. We note for future use that only the
functions
for 8 steps of cascading procedure. We note for future use that only the
functions
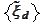 are affected by the numerical instability because these are obtained via
multiplication of
are affected by the numerical instability because these are obtained via
multiplication of
 with large-valued matrixes
with large-valued matrixes
 .
The functions
.
The functions
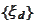 are obtained via multiplication with
are obtained via multiplication with
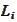 and, thus, are calculate with significantly better precision.
and, thus, are calculate with significantly better precision.
Our final remark is about extending results for scaling parameter
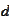 to
to
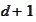 .
Note that
.
Note that
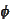 and
and
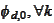 may be used interchangeably to construct MRA (GMRA for pair). The spaces
may be used interchangeably to construct MRA (GMRA for pair). The spaces
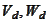 would be the same after shifting the parameter
would be the same after shifting the parameter
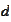 .
Hence, we can recover boundary functions for
.
Hence, we can recover boundary functions for
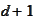 by scaling and shifting the
by scaling and shifting the
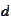 -scale
boundary functions. We obtain the boundary functions
-scale
boundary functions. We obtain the boundary functions
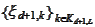 by applying the operation
by applying the operation
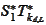 to the functions
to the functions
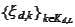 for some translation parameter
for some translation parameter
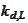 .
The
.
The
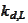 is selected by comparing
supports:
is selected by comparing
supports:
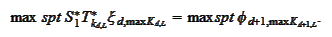 We perform a similar operation on the
right:
We perform a similar operation on the
right:
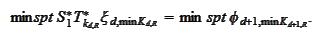
|